介电常数 - 科普新疆_新疆本地化科普资源共享开放平台

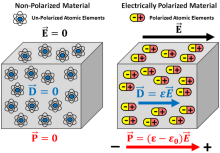
在电磁学中，介电常数通常指的是绝对介电常数，用ε表示。在电场中的电介质中的电荷会在电场的作用下出现微小的位移，从而出现束缚电荷；这是电介质内的位移极化。在极性材料中，分子存在固定的电偶极矩。不加外场时，由于分子的随机热运动，材料平均的电偶极矩为零。当加上电场时，这些电偶极矩的取向倾向于沿着电场方向，从而使得平均电偶极矩不为零，这是极性材料的取向极化。我们研究的多数电介质都可以近似地认为极化矢量与电场成正比，此时我们可以用介电常数度量在相同电场下电介质极化能力的强弱。

介电常数的量纲是I2T4M**-1L-3，国际单位制中介电常数的单位是F·m**-1（法拉/米）。通常，我们还会用相对介电常数来表示电介质的极化能力。相对介电常数是一个无量纲的数，定义是介电常数与真空介电常数之比

εr=ε/ε0 (1)

理想情况下，真空的相对介电常数是1。标准温度和压力下，空气的介电常数约为1.0006，一般情况下可以近似等于1。

定义

介电常数的定义是极化矢量与电场之比。极化矢量是电偶极矩的体密度，即

对于大多数电介质，我们可以近似地认为极化矢量与电场成正比，比例系数是极化率

其中是极化率。因此在电介质中，第一个麦克斯韦方程可以写成 $%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BE%7D%3D%5Cfrac%7B%5Crho_f%2B%5Crho_b%7D%7B%5Cvarepsilon_0%7D%3D%5Cfrac%7B%5Crho_f-%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BP%7D%7D%7B%5Cvarepsilon_0%7D%5CRightarrow%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cleft%5B%5Cvarepsilon_0%5Cleft%281%2B%5Cchi%5Cright%29%5Cvec%7BE%7D%5Cright%5D%3D%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BD%7D%3D%5Crho_f%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft%284%5Cright%29$

其中表示自由电荷，是由极化产生的束缚电荷。推导中用到了公式,该公式的推导详见本词条中的目录“束缚电荷”。我们定义了一个物理量：电位移矢量

这是介电常数的定义。真空中。介电常数与电磁波波速的关系是 $c%3D%5Cfrac%7B1%7D%7B%5Csqrt%7B%5Cvarepsilon%5Cmu%7D%7D$ ，推导详见目录“麦克斯韦方程组”和词条“电磁波”。

电介质中的静电学

束缚电荷

物理解释

电介质处于电场中时，其中的正电荷会受到沿着电场方向的力，负电荷受到的力相反。那么正负电荷之间会错开一个小的位移。在电介质内部的极化产生的电荷相互抵消，只有介质表面会有正负电荷的积累，这被称为“束缚电荷”。

公式推导

对于单个电偶极子，其产生的电势为 $V%5Cleft%28%5Cvec%7Br%7D%5Cright%29%3D%5Cfrac%7B1%7D%7B4%5Cpi%5Cvarepsilon_%7B0%7D%7D%5Cfrac%7B%5Cvec%7Bp%7D%5Ccdot%5Chat%7Br%7D%7D%7Br%5E%7B2%7D%7D%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%286%29$

根据极化矢量的定义，极化产生的电偶极矩是，因此在电介质中束缚电荷产生的电势是 $V%3D%5Cfrac%7B1%7D%7B4%5Cpi%5Cvarepsilon_%7B0%7D%7D%5Cint%5Cfrac%7B%5Cvec%7BP%7D%5Ccdot%5Chat%7Br%7D%7D%7Br%5E%7B2%7D%7DdV%20%5C%20%5C%20%20%5C%20%5C%20%5C%20%5C%20%20%5C%20%5C%20%5C%20%5C%20%287%29$

注意到 $%5Cvec%7B%5Cnabla%7D%5Cleft%28%5Cfrac1r%5Cright%29%3D%5Cfrac%7B%5Chat%7Br%7D%7D%7Br%5E2%7D$ ，应用矢量分析公式和散度定理可以得到 $V%3D%5Cfrac%7B1%7D%7B4%5Cpi%5Cvarepsilon_0%7D%5CBigg%28%5Ciint%5Cfrac%7B%5Cvec%7BP%7D%5Ccdot%20d%5Cvec%7BS%7D%7D%7Br%7D-%5Ciiint%5Cfrac%7B%5Cvec%7B%5Cnabla%7D%5Ccdot%5Cvec%7BP%7D%7D%7Br%7DdV%5CBigg%29%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%20%288%29$

分析上述公式的物理意义，我们可以看到，第一项表示面电荷的贡献，束缚电荷面密度是

其中是法向矢量。第二项表示像体电荷的贡献，像体电荷的电荷密度是

电容

电容的定义是器件带电量与电极两端电压之差之比，即 $C%3D%5Cfrac%7BQ%7D%7BU%7D$ 。存在电介质时此处的是自由电荷。根据（4）式，我们可以得到平行板电容器的电容 $C%3D%5Cvarepsilon%5Cfrac%7BA%7D%7Bd%7D%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft%2811%5Cright%29$

高斯定律

第一个麦克斯韦方程讲的是高斯定律。根据（4）式，对两边进行体积分即可得到电介质中的高斯定律 $%5Ciint%5Cvec%7BE%7D%5Ccdot%20d%5Cvec%7BS%7D%3D%5Cfrac%7BQ%7D%7B%5Cvarepsilon%7D%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%2812%29$

其中表示积分的闭合曲面内的自由电荷。因此，我们可以得到在电介质中的点电荷产生的电场是 $E%3D%5Cfrac%7Bq%7D%7B4%5Cpi%5Cvarepsilon%20R%5E2%7D%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%2813%29$

麦克斯韦方程组

在电磁介质中，我们经常会用到辅助物理量电位移矢量和磁场，因此经常会用到用表示的麦克斯韦方程组。描述电场与电荷密度关系的麦克斯韦方程可以写成如下形式

描述电流和电场的变化产生磁场的方程是 $%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BB%7D%3D%5Cmu_0%5Cvec%7BJ%7D%2B%5Cvarepsilon_0%5Cmu_0%5C%3A%5Cfrac%7B%5Cpartial%5Cvec%7BE%7D%7D%7B%5Cpartial%20t%7D%20%5C%20%5C%20%5C%20%5C%20%5C%20%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%2815%29$

在电磁介质中，电流密度可以分成三部分：自由电荷的电流；磁化产生的束缚电流；以及束缚电荷的电流 $%5Cvec%7BJ%7D_%7Bp%7D%3D%5Cfrac%7B%5Cpartial%5Cvec%7BP%7D%7D%7B%5Cpartial%20t%7D$ 。应用磁场的定义 $%5Cvec%7BH%7D%3D%5Cfrac%7B%5Cvec%7BB%7D%7D%7B%5Cmu_%7B0%7D%7D-%5Cvec%7BM%7D$ ，我们可以用和写出第四个麦克斯韦方程 $%5Cvec%7B%5Cnabla%7D%5Ctimes%5Cvec%7BH%7D%3D%5Cvec%7BJ%7D_f%2B%5Cfrac%7B%5Cpartial%5Cvec%7BD%7D%7D%7B%5Cpartial%20t%7D%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft%2816%5Cright%29$

斯塔克效应

斯塔克效应是在量子力学中在恒定电场中的极化。为了简单起见，我们考虑氢原子在z方向的电场中的极化。氢原子的电势能是

我们将用微扰论计算这个势能中波函数的修正。下面我们考虑能级1s的波函数的偏移。由于算符z的宇称是奇的，因此矩阵元。因此我们要考虑二阶微扰的效应。对于二阶微扰，能级的修正是 $%5Cvarepsilon_2%3Dq%5E2E%5E2%5Csum_%7Bn%5Cneq1%2Clm%2C%7D%5Cfrac%7B%5Cleft%7C%5Cleft%5Clangle100%5Cright%7Cz%5Cleft%7Cnlm%5Cright%5Crangle%5Cright%7C%5E2%7D%7BE_1-E_n%7D%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%2818%29$

考虑了微扰之后的波函数是 $%5Cleft%7C%5Cpsi%5Cright%5Crangle%3D%5Cleft%7C%5Cbegin%7Bmatrix%7D100%5C%5C%5Cend%7Bmatrix%7D%5Cright%5Crangle-qE%5Csum_%7Bn%5Cneq1%2Clm%7D%5Cfrac%7B%5Cleft%5Clangle%20nlm%5Cright%7Cz%5Cleft%7C%5Cbegin%7Bmatrix%7D100%5C%5C%5Cend%7Bmatrix%7D%5Cright%5Crangle%7D%7BE_1-E_n%7D%5Cleft%7C%5Cbegin%7Bmatrix%7Dnlm%5C%5C%5Cend%7Bmatrix%7D%5Cright%5Crangle%2B%5Ccdots%20%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%20%2819%29$

因此，电偶极矩是 $%5Cleft%5Clangle%5Cpsi%5Cleft%7Cqz%5Cright%7C%5Cpsi%5Cright%5Crangle%3D-2q%5E2E%5Csum_%7Bn%5Cneq1%2Clm%7D%5Cfrac%7B%5Cleft%7C%5Cleft%5Clangle%20nlm%5Cright%7Cz%5Cleft%7C100%5Cright%5Crangle%5Cright%7C%5E2%7D%7BE_1-E_n%7D%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%2820%29$

相应地，我们可以得到摄化率 $%5Cchi_%7B1s%7D%3D-2q%5E%7B2%7D%5Csum_%7Bn%5Cneq1%2Cl%2Cm%7D%5Cfrac%7B%5Cleft%7C%5Cleft%5Clangle%20nlm%5Cright%7Cz%5Cleft%7C100%5Cright%5Crangle%5Cright%7C%5E%7B2%7D%7D%7BE_%7B1%7D-E_%7Bn%7D%7D$ .

随时间变化电场中的电介质

材料受到外场作用时不会瞬间极化，电介质极化更普遍的表达式是

这是线性相应理论对极化过程的描述。应用卷积定理，可以得到

也就是说电介质的极化依赖于外加电场的频率，极化率会有一个色散关系。

复介电常数

材料对外部电场的线性响应通常与场的频率一致。电位移矢量的变换频率与电场的变化频率是相同的。而施加电场后，极化需要时间，这反应在电位移矢量和电场之间存在一个相位差。因此，通常介电常数是一个复数，即