科普中国-复势

由速度势作实部，流函数作虚部构成的解析函数W(z)称为复势。3设有一不可压缩流体做平面定常运动，其速度向量v=(u,v)，其中无源、无汇，也无涡流。这些说明它等价于v=u+iv，为解析函数，称为流体的复速度，其与积分路径无关，称为流体的复势。

概念

在势流中，问题一般涉及在适当的边界条件下解拉普拉斯方程 和 。合适的边界条件通常是：在无穷远处流动均匀或为零，和流体不能穿过它所绕流的固体表面。然而，除了对于某些简单形状 和 可以解调和方程或直接积分 容易地求得外，在速度已知时，最好用复变量理论和保角变换来确定 和 。1

基本原理

复函数

在二维问题中，定义一个函数 （称为复势）的充要条件是 和 为调和函数及满足柯西-黎曼方程。复函数定义为：

式中 及 。在复平面 中， 和 形成一个矩形坐标网络。我们考虑 和 是复变量 的函数，以 代替 和 。平面 代表物理流动平面。

一般

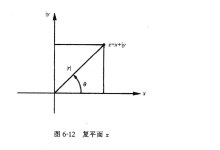
见图1-1， 为具有实数部分 和虚数部分 的复数， 可以写作为 的函数，因此， 的实数部分为 及虚数部分为 。

柯西-黎曼条件连同 和 单值及 和 的所有偏导数连续等条件意味着 是可析（或正则）函数。可析函数 是这样的函数，（1）在一封闭廓线 内为有限值并为单值，及（2）所有导数存在并为单值。一个 的可析函数的实数部分和虚数部分称为共轭函数并且是调和的。 和 是共轭函数并且我们知道 。

参照图1-1， 可以对任意 进行计算。如果我们取 平行于 轴，我们有 及

如果取 平行于 轴，我们有 并且

因此两个表达式中无论哪一个都可以应用，而且两者必定相等，因此，我们由令它们的实数和虚数部分分别相等得到柯西-黎曼条件：

和

复速度

对复函数 微分，我们得到

或

称为复速度。

保角变换

发生运动的物理平面是或平面，在该平面，为常数的线为曲线并且代表流线。在平面中， 和形成正交网络。可以通过一个保持 和正交性质的转换将流动从